The Journal of Personality and Social Psychology: The Good, The Bad, and The Ugly

The Journal of Personality and Social Psychology is one of the main outlets for social and personality psychologists. It publishes around 110 empirical articles a year (and a small number of other types of articles) and is considered a prestigious outlet. It is also often criticized. That’s to be expected. As the Dutch saying goes: “High trees catch a lot of wind”.

For example, Simonsohn, Nelson, and Simmons validated their p-curve technique on articles that reported ANCOVA’s in JPSP. They found that if you look at a random selection of articles in JPSP that report ANCOVA’s, the pattern of results is what you would expect if there is no effect whatsoever, and we selectively publish Type 1 errors. JPSP also published the famous article on pre-cognition by Daryl Bem, and then desk-rejected a set of studies failing to replicate the original findings because they did not want to be the "Journal of Bem replication”. This is not very good.

Since these events, I have developed the habit of talking about JPSP as a journal that is prestigious, but not high quality. After recently reading a particularly bad article in JPSP, I said on Twitter that I thought JPSP was a 'crap journal', but Will Gervais correctly pointed out I can hardly conclude this based on n = 1. And if I'm honest, I believe it can't all be bad. So the truth must be somewhere in the middle. But where in the middle? I decided to take a quick look at the last 4 issues of JPSP (November, December, January, and February 2017/2018) to see if I was being unreasonably critical. So let’s go through the Good, The Bad, and the Ugly.

The Good

JPSP publishes a very special type of empirical article, which we might call the Odyssey format. They rarely publish single study papers, and most articles have between 4 and 7 empirical studies. Because these articles have a lot of studies, they can cover a lot of ground (such as The Good, The Bad, and The Ugly of Moral Affect, for example). I like this. It has potential to publish a coherent set of studies that really test a hypothesis thoroughly, and provide convincing support for an idea. Regrettably, the journal rarely lives up to this potential, but the format is good. If JPSP would require more replication and extension studies, where all studies use similar and well-validated measures, and if it would move further away from publishing sets of tangentially related conceptual replications, it could work. It’s an accomplishment that a journal can convince researchers to combine 7 studies into a single paper, instead of publishing 3 different papers, in this day and age.

It should not be a surprise that getting researchers to publish all their studies together leads to an outlet with a high impact factor. There are more reasons to cite an article that discusses The Good, The Bad, and The Ugly of X, than an article that discusses The Good of X. I’d say that simply based on the quantity of studies, JPSP should have an impact factor that is at least twice that of any journal that publishes single study papers – there’s just way more to cite. Furthermore, almost all articles are cited after a few years, with median citation counts from 2012 to 2017 currently being 33, 20, 16, 11, 5, and 2 (based on data I downloaded from Scopus). Remember that you can’t make statements about single articles or single researchers based on the performance of a journal (see and sign the DORA declaration). For example, I published a paper on equivalence testing in SPPS in 2017, which according to SCOPUS has 20 citations so far. This is more than any article published in JPSP in 2017.  So when evaluating a job applicant, I see no empirical justification to consider any single paper in JPSP better than any single paper in another journal (especially given The Ugly section below).

The journal consists of 3 sections. It took me a while to figure out how to identify them (the information in which section an article was published is not part of the bibliometric info) but the journal starts with a section on attitudes and social cognition, follows with a section on interpersonal relations and group processes, and ends with a section on personality processes and individual differences. The first article in the section has a header with the section name in the PDF, but unless you look for it, there is no way to know which section a paper was published in. This matters because the last section (on personality processes and individual differences) is rock solid. The other two sections are not unequivocally good, even though there are nice articles in these sections as well. If I was working in the personality processes and individual differences section of JPSP, I would split off from the journal (and roll over to a free open access publisher), and publish 4 instead of 10 issues a year filled with only articles on personality processes and individual differences. But I guess that's me.

The Bad

As far as I can see, what sets JPSP apart from other journals is that they publish huge articles with way more studies per article than other outlets, and they are in a position to reject articles that are unlikely to appeal to a large audience (and thus, get cited less). But that’s it. The studies that are done are not better than those in other outlets – there are just more of them.

If we ignore the theoretical content, and focus on the methodological content, there is really nothing to write home about in JPSP. A depressingly large number of studies relies exclusively on Null-Hypothesis Significance Testing, performed badly. In a majority of papers (and sorry if you are the exception – I love you!) interpretations are guided by p < .05 or p > .05. A p = .13 is the absence of an effect, p = 0.04 is an effect (see Lakens, Scheel, & Isager, 2018, on how to prevent this mistake). Effect sizes are sometimes not even reported, but if they are, they are literally never interpreted. Measures that are used are often ad hoc, not validated, and manipulations are often created for a single study but not extensively pilot tested or validated. There are a lot of studies, but the relationship between studies is almost always weak. The preferred approach is ‘now we show X in a completely different way’, whereas the potential of the JPSP format lies in ‘here we use the same validated measures across a set of studies with carefully piloted manipulations to show X’. But this rarely happens. As far as I could see when going through the papers, raw data availability is not zero, but very low (it would be super useful if JPSP used badges to clearly communicate where data is available, as some researchers recently proposed in an open letter to the then incoming editor of the first section of JPSP).

There is no reason to expect authors to use better methods and statistics in their work that ends up in JPSP, unless the editors at JPSP would hold these authors to higher standards. They don’t. I’m an editor at other journals (which might be a COI except I really don't care about journals in psychology and mainly read preprints), and I saw a lot of things I wouldn’t let authors get away with. Sample size justifications are horribly bad, power analyses (in the rare cases they are performed) are done incorrectly, and people who publish in (the first two sections of) JPSP generally love MTurk.

You might say that it’s just a missed opportunity that JPSP does not meet its potential and just publishes ‘more’. But there is another Bad. If we value a 7 study article in JPSP more than a 2 study article in another outlet, we will reward researchers who have lots of resources more than researchers with less resources. Whether or not you can perform 7 studies depends on how much money you have, the size of your participant pool, whether you have student assistants to help you or not, etcetera. So when evaluating a job applicant, I see no empirical justification to consider any single paper in JPSP with 7 studies as a better accomplishment than any single paper in another journal with 2 studies, without taking into account the resources the applicant had. It will not be a perfect correlation, but I predict that if you have more money, you will get more JPSP articles.

The Ugly

So one important question for me was: Is JPSP still publishing papers in which researchers increase their Type 1 error rate through p-hacking? Or is there, beyond the rare bad apple, mainly high quality work in JPSP? I took a look at four recent issues (November, December, January, and February 2017/2018). I evaluated all articles in the February issue, and checked how many articles in the other 3 issues raised strong suspicions of p-hacking. Being accused of p-hacking is not nice. Trust me, I know. But people admit they selectively report and p-hack (Fiedler & Schwarz, 2015, John et al., 2012), and if you read the articles in JPSP that I think are p-hacked, I doubt there will be much disagreement. If you wrote one of these articles, and are unaware of the problems with p-hacking, I'd recommend enrolling in my MOOC.

The articles in the personality processes and individual differences looked much better. This is to a large extent because the studies rarely rely on the outcome of a single DV measured after an experimental manipulation in a too small sample. The work is more descriptive, datasets are typically larger, and thus there is no need to selectively report what ‘works’. I’m not an expert in this field, so there might be things wrong with these papers that I was oblivious to, but to me these papers looked good.

I also skipped one article about artificial intelligence tools can detect whether someone is gay – the study is under ethical review and so problematic I thought it was fair to ignore it. Although I guess the study would deserve to fall under The Ugly.

This leaves 6 articles in the first two sections of the February issue. At the end of this post you can see the main tests for each study (copy pasted from the HTML version of the articles) and some comments about sample sizes, and my evaluation, if you prefer more detail about the basis of my evaluation. It’s obviously best to read the articles yourself. Of these 6 articles, two examined hypotheses that were plausible, and did so in a convincing manner. For example, an article showed that participants judged targets who they know performed immoral actions (broadly defined) as less competent.

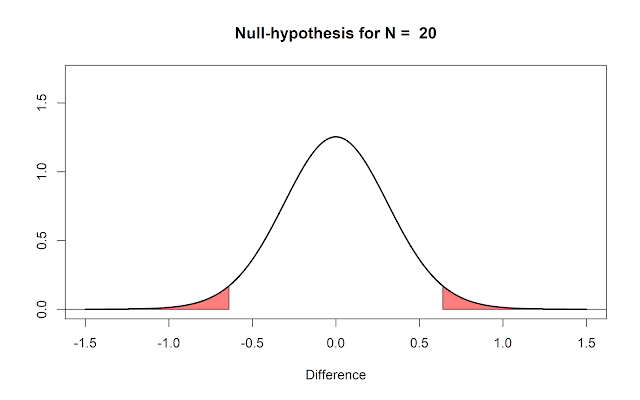
The four other papers revealed the pattern I had feared. A logical question is: How can you identify a set of studies that is p-hacked? If the p-values in JPSP were realistically distributed, the distribution should look something like the curve in the picture below. Some predicted p-values should fall above .05, some fall below (indicated by the red area). Papers can have a surprising number of of p-values just below .05, when we should expect much smaller p-values (e.g., p = 0.001) often when there are true effects. This is in essence what p-curve analysis tests (or see TIVA by Uli Schimmack, and this recent blog by Will Gervais for related ideas). I don't present a formal p-curve analysis (although I checked some papers statistically), but in essence, I believe the pattern of p-values is unrealistic enough to cause doubt in objective readers with sufficient knowledge about what p-values across studies should realistically look like, especially in combination with a lack of pre-registration, and when many different dependent variables are reported across studies (and not all DV's are transparently reported). I want to make it clear that it might be possible, although very rare, that a single paper shows this surprising pattern of p-values even had every analysis been pre-registered - but there are too many papers like this in JPSP. If you published one of the articles I think was p-hacked and want to argue you did nothing wrong, that's fine with me. If everyone wants to do this, that's just not possible.

 

The studies that concern me showed that all predictions worked out as planned, even though sample sizes were decided upon quite randomly, and for all tests (or mediation models) p-values were just below .05. For example, DelPriore, Proffitt Leyva, Ellis, & Hill (2018) examined the effects of paternal disengagement on women’s perceptions of male mating intent. Their pattern of results across studies is Study 1, p = .030, Study 2, p = .049, Study 3, p = .04 and p = .028, Study 4, p = .019 and p = .012, Study 5, b = .09 (SE = .05), percentile 95% CI [.002, .18] (see how close these CI are to 0). Now, it is possible that couple of reviewers and an editor can miss the fact that this pattern is not realistic if they have not educated themselves on these matters somewhere during the last 5 years, but they really should have if they want to publish high quality work. Or take Stellar, Gordon, Anderson, Piff, McNeil, & Keltner (2018) who studies awe and humility. Study 1: p = .04, and p = .01, Study 2: p < .001, when controlling for positive affect, p = .02, Study 3: p = .02, Study 4: p < .001 and p = .03, Study 5: “We found a significant path from the in vivo induction condition (neutral = 0, awe = 1) to humility, via awe and self-diminishment (95% CI [0.004, 0.22]; Figure 4). (It’s amazing how close these CI can get to 0).

I don’t want to generalize this to all JPSP articles. I don’t intend to state that two-thirds of JPSP articles in the first two sections are p-hacked. I (more quickly) went through the 3 issues published before the February issue, to see if the February issue was some kind of fluke, but it isn't. Below are examples of articles with unrealistic patterns of p-values in the November, December, and January issues.

Issue 114(1)

Hofer, M. K., Collins, H. K., Whillans, A. V., & Chen, F. S. (2018). Olfactory cues from romantic partners and strangers influence women’s responses to stress. Journal of Personality and Social Psychology, 114(1), 1-9. In study 1, 96  couples, main result: “There was a nonsignificant main effect of scent exposure, F(2, 93) = 1.15, p = .32, η2  = 0.02, which—of most relevance for our hypothesis—was qualified by a significant interaction between time and scent exposure, F(5.36, 249.44) = 2.26, p = .04, η2  = 0.05.” Other effects: During stress recovery, women exposed to their partner’s scent reported significantly lower perceived stress than both those exposed to a stranger’s or an unworn scent (M = 20.25, SD = 14.96 vs. M = 27.14, SD = 16.67 and M = 29.01, SD = 14.19; p = .038 and .015, respectively, Table 1). Cortisol: There was a nonsignificant main effect of scent exposure, F(2, 93) = 0.83, p = .44, η2  = 0.02, which—of most relevance for our hypotheses—was qualified by a significant interaction between time and scent exposure, F(2.83, 131.76) = 3.05, p = .03, η2  = 0.06.

Issue 113(4)

Cortland, C. I., Craig, M. A., Shapiro, J. R., Richeson, J. A., Neel, R., & Goldstein, N. J. (2017). Solidarity through shared disadvantage: Highlighting shared experiences of discrimination improves relations between stigmatized groups. Journal of Personality and Social Psychology, 113(4), 547-567. Study 1: p = .078, Study 2: p = .001, and p = .010, Study 3: p = .031, p = .019, and p = .070, p = .036, and p = .120, Study 4: p = .030, p = .017, p = .014, and p= .040, Study 5: p = .020, p = .045 and p = .016.

Savani, K., & Job, V. (2017). Reverse ego-depletion: Acts of self-control can improve subsequent performance in indian cultural contexts. Journal of Personality and Social Psychology, 113(4), 589-607. Study 1A: p = .018, Study 1B: p = .049, Study 1c: p = .031, Study 2: p = .047. and p = .051, Study 3: p = .002 and p = .006 (this looks good, the follow up analysis is p = .045). Study 4: p = .023; p = .018; and p = .003.

Issue 113(3)

Chou, E. Y., Halevy, N., Galinsky, A. D., & Murnighan, J. K. (2017). The goldilocks contract: The synergistic benefits of combining structure and autonomy for persistence, creativity, and cooperation. Journal of Personality and Social Psychology, 113(3), 393-412. Study 1: p = .01, p = .007, p = .05, Study 2: manipulation check: p = .05. main result: p = .01, p = .02, p = .01 and, p = .08, p = .06, and p = .03. Study 3a: manipulation check: p = .03. Main result: p = .05, p = .02, p = .06. Study 3b: p = .04, p = .02, p = .02. Study 3C: p = .08, Study 4: p < .001, p = .01, Study 5A: p = .03, p = .03, p = .03, Study 5B: p = .01, p = .05. Experiment 6. p = .03.

Conclusion

I would say that something is not going right at JPSP. The journal has potential, in that it has convinced researchers to submit a large number of studies, consisting of a line of research, instead of publishing single study papers. And even despite the fact that most sets of studies lack strong coherence, are weak in sample size justification, validation of manipulations, and the choice of measures, there are some good articles published in the first two sections (the last section is doing fine).

However, there is a real risk that if you encounter a single article from JPSP, it is p-hacked and might just be a collection of Type 1 errors. You can easily notice this if you simply look at the main hypothesis tests in each study (or all tests in a mediation model).

When evaluating a job candidate, you can not treat a JPSP article as a good article. The error rate of making such statements will be too high. Especially in the first two sections, there is (based on my rather limited sampling, but still) a much higher error rate than 5% (enter a huge confidence interval here – if anyone wants to go through all issues, be my guest!) if you would attempt such simplistic evaluations of the work people have published. Now you should never evaluate the work of researchers just based on the outlet they published in. I’m just saying that if you would use this as a heuristic, you’d also be quite often wrong when it comes to JPSP.

This is regrettable. I’d like a journal that many people in my field consider prestigious and a flagship journal to mean something more than it currently does. High standards when publishing papers should mean more than ‘As an editor I counted the number of studies and there are more than 4 and I think many people are interested in this’. I hope JPSP will work hard to improve their editorial practices, and I hope researchers who publish in JPSP will not believe their work is high quality (remember that regardless of p-hacking, most studies had weak methods and statistics), but critically evaluate how they can improve. If JPSP is serious about raising the bar, there are straightforward things to do. Require a good sample size justification. Focus more on the interpretation of effect sizes, and less on p-values. Look for articles that use the same validated manipulations and measures consistently across studies. Publish (preferably preregistered) studies with mixed results, because not every prediction should be significant even when examining a true effect. And make sure the p-value distribution for all key hypothesis tests looks realistic. There has been so much work on improving research practices in recent years, that I expected a flagship journal in my field would have done more by now. 



Thanks to Will Gervais for motivating me to write this blog, and to Will, Farid Anvari and Nick Coles for feedback on an earlier draft.

If you are interested, below is a more detailed look at the articles I read while preparing this blog post.

Attitudes and social cognition

Stellar, J. E., & Willer, R. (2018). Unethical and inept? the influence of moral information on perceptions of competence. Journal of Personality and Social Psychology, 114(2), 195-210.

General idea: Across 6 studies (n = 1,567), including 2 preregistered experiments, participants judged targets who committed hypothetical transgressions (Studies 1 and 3), cheated on lab tasks (Study 2), acted selfishly in economic games (Study 4), and received low morality ratings from coworkers (Study 5 and 6) as less competent than control or moral targets.

All studies show this convincingly. There is an OSF project where all data and materials are shared, which is excellent: https://osf.io/va6bj/?view_only=1220367fb74e44a4a15c0d8ef3cdfbf4. I think the hypothesis is very plausible (and even unsurprising). I want to point out that this is a very good paper, because I am less positive about another paper by the same first author in the same issue. But this is a later paper, so overall, it seems we are seeing progress in ways of working, which makes me happy.

Olcaysoy Okten, I., & Moskowitz, G. B. (2018). Goal versus trait explanations: Causal attributions beyond the trait-situation dichotomy. Journal of Personality and Social Psychology, 114(2), 211-229.

From the abstract: Participants tended to attribute the cause of others’ behaviors to their goals (vs. traits and other characteristics) when behaviors were characterized by high distinctiveness (Study 1A & 1B) or low consistency (Study 2). On the other hand, traits were ascribed as predominant causal explanations when behaviors had low distinctiveness or high consistency. Study 3 investigated the combined effect of those behavioral dimensions on causal attributions and showed that behaviors with high distinctiveness and consistency as well as low distinctiveness and consistency trigger goal attributions.

Evaluation: Good. The effects are all very large, and I would say had a very high prior. It would have been nice if data and materials would have been shared (especially the materials, to evaluate how surprising the data were, given the materials used).

Woolley, K., & Risen, J. L. (2018). Closing your eyes to follow your heart: Avoiding information to protect a strong intuitive preference. Journal of Personality and Social Psychology, 114(2), 230-245.

Main hypothesis: We predict that people avoid information that could encourage a more thoughtful, deliberative decision to make it easier to enact their intuitive preference.

Study 1: Sample 300 MTurk workers. Post-hoc power analysis. Main result: “As predicted, a majority of participants (62.7%; n = 188) chose to avoid calorie information, z = 4.33, p < .001, 95% CI = [56.9%, 68.2%].” But this is a nonsensical test against 50%. Why would we want to test against 50%? It makes no sense.

Study 2A: Sample 150 guests at a museum. Main result: “We found the predicted effect of payment information, β = −.63, SE = .27, Wald = 5.45, p = .020, OR = .53, 95% CIExp(B) = [.32, .90].” Regrettably, the authors interpret a p = 0.183 as evidence for the absence of an effect: “As predicted, there was no interaction between choice of information and bonus amount, β = .36, SE = .27, Wald = 1.78, p = .183, OR = 1.43, 95% CIExp(B) = [.85, 2.42],” This is wrong.

Study 2B: Sample 300 MTurkers. Main result: “As predicted, the stronger participants’ intuitive preference for the cartoon task, the more they avoided the bonus information, β = .23, SE = .07, Wald = 9.61, p = .002, OR = 1.26, 95% CIExp(B) = [1.09, 1.45].” This seems quite expected.

Study 3: 200 guests at a museum. Main result: “ndeed, using a chi-square analysis we found that people avoid information more when offered an opportunity to bet that a student would do poorly (57.8%) than when offered a chance to bet that a student would do well (42.9%), χ2 (1, N = 200) = 4.49, p = .034, φ = .15, OR = 1.83, 95% CIExp(B) = [1.04, 3.21].”

Study 4a: Sample 200 Mturkers. Main result: “As predicted, there was greater information avoidance in the plan-choice condition when the information was relevant to the decision (58.4%)  [  8  ]  than in the plan-assigned condition (41.4%), χ2 (1, N = 200) = 5.78, p = .016, φ = .17, OR = 1.99, 95% CIExp(B) = [1.13, 3.49].”

Study 4b: Sample size is doubled from 4a. Main result: A chi-square analysis of condition (assigned to information or not) on choice (Plans A-C vs. Plan D) revealed the predicted effect. More participants selected Plan D, the financially rational option, when assigned to receive information (59.6%, n = 121), than when assigned no information (48.0%, n = 95), χ2 (1, N = 401) = 5.45, p = .020, φ = .12, OR = 1.60, 95% CIExp(B) = [1.08, 2.38].

Study 5: 200 guests at a museum. Main result: “We first tested our main prediction that information avoidance is greater when it can influence the decision. As predicted, more people chose to avoid information when offered an opportunity to accept or refuse a bet that a student would do poorly (61.2%) than when assigned to bet that a student would do poorly (43.4%), χ2 (1, N = 197) = 6.25, p = .012, φ = .18, OR = 2.06, 95% CIExp(B) = [1.17, 3.63].”

Evaluation: Some tests are nonsensical – such as the test against 50% in Study 1. Weird that passed peer review. Everything else works out way too nicely. All critical p-values are either good (but then the test is kind of trivial as in Study 1) or all between the .01-.05 range, which is not plausible. This does not look realistic. This pattern of p-values suggest massive selective reporting, and flexibility in the data analysis to yield p < .05.  

Interpersonal relations and group processes,

Stellar, J. E., Gordon, A., Anderson, C. L., Piff, P. K., McNeil, G. D., & Keltner, D. (2018). Awe and humility. Journal of Personality and Social Psychology, 114(2), 258-269.

Main idea: “We hypothesize that experiences of awe promote greater humility. Guided by an appraisal-tendency framework of emotion, we propose that when individuals encounter an entity that is vast and challenges their worldview, they feel awe, which leads to self-diminishment and subsequently humility.”

Study 1: 119 freshmen, no justification for sample size. Main result: “In keeping with Hypothesis 1, participants who reported frequent and intense experiences of awe were judged to be more humble by their friends controlling for both openness and positive affect, r(92) = .22, p = .04, as well as openness and a discrete positive emotion—joy, r(92) = .25, p = .01.  [  2  ]  These two analyses generally remained significant when we added liking as an additional control variable, positive affect: r(91) = .18, p = .09; joy: r(91) = .21, p = .05.”

Study 2: Sample: 106 same freshmen from Study 1. Authors do not report all measures that were collected (“Embedded among other self-report items not relevant to this study”). Main result: Feeling humble and awe is correlated. No doubt, but almost no care to control for confounds, and only including positive affect is almost enough to make the effect disappear: Participants reported feeling more humble on days when they experienced more awe, B = .18, t(176) = 6.56, p < .001). This effect held when controlling for positive affect, B = .07, t(1178) = 2.31, p = .02, and when controlling for the prosocial emotion of compassion, B = .13, t(197) = 4.71, p < .001.

Study 3: Sample 104 adults, 14 excluded for non-preregistered reasons. Main result: “Participants in the awe and neutral conditions had a different balance between disclosing their strengths and weaknesses, t(84) = 2.38, p = .02.”

Study 4: Sample 598 adults from MTurk. Main result: “Participants who recalled an awe experience reported a significantly larger amount of their success coming from external forces compared with the self (M = 55.28, SD = 25.89) than those who wrote about a neutral (M = 44.03, SD = 21.50), t(593) = 4.78, p < .001), or amusing experience (M = 50.27, SD = 23.79), t(593) = 2.12 p = .03.” Mediation model is similarly hanging on a thread.

Study 5: Sample: 93 undergraduates, no justification. Mediation model: “We found a significant path from the in vivo induction condition (neutral = 0, awe = 1) to humility, via awe and self-diminishment (95% CI [0.004, 0.22]; Figure 4).” It’s amazing how close these CI can get to 0.

Evaluation: Everything works out for these authors, and that without sample size planning. This is simply not realistic. I believe almost all critical tests in this paper are selectively reported, and there are clear signs of flexibility in the data analysis to yield p < .05.  

Webber, D., Babush, M., Schori-Eyal, N., Vazeou-Nieuwenhuis, A., Hettiarachchi, M., Bélanger, J. J., . . . Gelfand, M. J. (2018). The road to extremism: Field and experimental evidence that significance loss-induced need for closure fosters radicalization. Journal of Personality and Social Psychology, 114(2), 270-285.

Study 1: Sample is 74 members suspected of a terrorist organization. Main result: “Analyses on the full sample first revealed a nonsignificant total effect between the predictor (LoS) and the outcome (extremism); b = .15, SE = .12, p = .217. Results next revealed that LoS predicted NFC; b = .26, SE = .13, p = .050; and that NFC subsequently predicted extremism; b = .36, SE = .10, p < .001. The direct effect of LoS on extremism was not significant; b = .06, SE = .11, p = .622. To examine the significance of the indirect effect, we calculated bias corrected 95% confidence intervals of the indirect effects using 10,000 bootstrapped resamples. As “0” was not contained within the confidence intervals, the indirect effect was indeed significant; 95% CI [.024, .215].”

Study 2: Sample: 237 (male) former members of the LTTE. Main result: “Analyses on the full sample revealed a significant total effect of LoS on extremism; b = .27, SE = .05, p < .001. Analyses further revealed that LoS was related to increased NFC; b = .27, SE = .11, p = .012; and NFC was related to increased extremism; b = .06, SE = .03, p = .048. The direct effect of LoS on extremism remained significant; b = .25, SE = .05, p < .001. Ninety-five percent confidence intervals obtained with 10,000 bootstrapped resamples revealed that the indirect effect was significant; 95% CI [.0001, .044]. Analyses on the reduced sample and including covariates revealed an identical pattern of results, and levels of significance were unchanged; 95% CI [.0004, .051].”

Study 3: Sample: 196 people through online websites. Main result: “Power analysis is based on a medium effect (which is bad practice). Main result: “Only the main effect of LoS condition was significant, such that participants in the LoS condition (M = 5.19; SE = .17) expressed significantly greater extremism than participants in the control condition (M = 4.63; SE = .17); F(1, 192) = 5.52, p = .020, η2  = .03.”

Study 4: Sample: 344 participants from Amazon Turk. Main result: “The total effect of LoS condition on endorsement of extreme political beliefs was not significant (p = .828). Analyses further revealed that participants in the LoS (vs. control) condition reported higher NFC; b = .24, SE = .08, p = .003; and NFC was related to increased extremism; b = .17, SE = .08, p = .028. The direct effect of LoS condition on extremism remained nonsignificant (p = .892). Ninety-five percent confidence intervals obtained with 10,000 bootstrapped resamples revealed a significant indirect effect, 95% CI [.006, .100].”

Evaluation: First of all, major credits for collecting these samples or people (suspected to be) involved in terrorist organizations. This is really what social psychology can contribute to the world. Regrettably, the data is overall not convincing. The data is not messy enough (across the 4 studies, everything that needs to work works) but very often things are borderline significant (think about a bootstrapped CI (which will vary a bit every time) that has a lower limit of .0001, reported to 4 decimals!). Still, major credits for data collection.

DelPriore, D. J., Proffitt Leyva, R., Ellis, B. J., & Hill, S. E. (2018). The effects of paternal disengagement on women’s perceptions of male mating intent. Journal of Personality and Social Psychology, 114(2), 286-302.

Main conclusion from abstract: Together, this research suggests that low paternal investment (including primed paternal disengagement and harsh-deviant fathering) causes changes in daughters’ perceptions of men that may influence their subsequent mating behavior.

Study 1, n1 = 34, n2 = 41. Substantial data exclusions without clear reasons. Not pre-registered. Main finding “However, there was a significant main effect of priming condition, F(1, 73) = 4.91, p = .030, d = .52.” No corrections for multiple comparisons.

Study 2, n1 = 35, n2 = 33. Main result: “As predicted, there was a significant simple main effect of condition on women’s perceptions of male sexual arousal, F(1, 65) = 4.01, p = .049, d = .49.”

Study 3, similar sample sizes, main result: “There was, however, a significant three-way interaction between priming condition, target sex, and target emotion, F(3, 81) = 2.82, p = .04. This interaction reflected a significant simple main effect of priming condition on women’s perceptions of male sexual arousal, F(1, 83) = 5.02, p = .028, d = .49,”

Study 4, where I just looked at the main result: “The analysis revealed a significant main effect of priming condition on women’s perceptions of the male confederate’s dating intent, F(1, 60) = 5.82, p = .019, d = .61, and sexual intent, F(1, 60) = 6.69, p = .012, d = .66.”

Study 5: “Both indirect pathways remained statistically significant: paternal harshness → perceived sexual intent → unrestricted sociosexuality: b = .09 (SE = .05), percentile 95% CI [.002, .18]; paternal harshness → residual father-related pain → perceived sexual intent: b = .04 (SE = .03), bias corrected 95% CI [.004, .12].” You can see how close these CI are to 0.

Finally, the authors perform an internal meta-analysis.

Evaluation: This does not look realistic. This pattern of p-values suggest massive selective reporting, and flexibility in the data analysis to yield p < .05.  

Personality processes and individual differences

Humberg, S., Dufner, M., Schönbrodt, F. D., Geukes, K., Hutteman, R., van Zalk, Maarten H. W., . . . Back, M. D. (2018). Enhanced versus simply positive: A new condition-based regression analysis to disentangle effects of self-enhancement from effects of positivity of self-view. Journal of Personality and Social Psychology, 114(2), 303-322.

Main idea (from abstract): “We provide a new condition-based regression analysis (CRA) that unequivocally identifies effects of SE by testing intuitive and mathematically derived conditions on the coefficients in a bivariate linear regression. Using data from 3 studies on intellectual SE (total N = 566), we then illustrate that the CRA provides novel results as compared with traditional methods. Results suggest that many previously identified SE effects are in fact effects of PSV alone.”

Evaluation. The materials are on the OSF, and it is primarily a new statistical technique (no new data was collected). It does not fall in the empirical studies I am examining, but it was a good paper.

Dejonckheere, E., Mestdagh, M., Houben, M., Erbas, Y., Pe, M., Koval, P., . . . Kuppens, P. (2018). The bipolarity of affect and depressive symptoms. Journal of Personality and Social Psychology, 114(2), 323-341.

Main idea (from abstract): “these findings demonstrate that depressive symptoms involve stronger bipolarity between positive and negative affect, reflecting reduced emotional complexity and flexibility.”

Evaluation: This was too far out of my domain to confidently evaluate. There were nice things in the article, pretty close replications across 3 experience sampling studies, a multiverse analysis to explore all possible combinations of items.

Siddaway, A. P., Taylor, P. J., & Wood, A. M. (2018). Reconceptualizing anxiety as a continuum that ranges from high calmness to high anxiety: The joint importance of reducing distress and increasing well-being. Journal of Personality and Social Psychology, 114(2), e1-e11.

Evaluation: I’ll keep this short, because unless I’m mistaking, this seems to be an electronic only replication study: “We first replicate a study by Vautier and Pohl (2009), who used the State–Trait Anxiety Inventory (STAI) to reexamine the structure of anxiety. Using two large samples (N = 4,138 and 1,824), we also find that state and trait anxiety measure continua that range from high calmness to high anxiety.” It’s good and clear.

Vol 114 (1)

Hofer, M. K., Collins, H. K., Whillans, A. V., & Chen, F. S. (2018). Olfactory cues from romantic partners and strangers influence women’s responses to stress. Journal of Personality and Social Psychology, 114(1), 1-9.

Study 1: 96  couples. Main result: “There was a nonsignificant main effect of scent exposure, F(2, 93) = 1.15, p = .32, η2  = 0.02, which—of most relevance for our hypothesis—was qualified by a significant interaction between time and scent exposure, F(5.36, 249.44) = 2.26, p = .04, η2  = 0.05.” Other effects: During stress recovery, women exposed to their partner’s scent reported significantly lower perceived stress than both those exposed to a stranger’s or an unworn scent (M = 20.25, SD = 14.96 vs. M = 27.14, SD = 16.67 and M = 29.01, SD = 14.19; p = .038 and .015, respectively, Table 1). Cortisol: There was a nonsignificant main effect of scent exposure, F(2, 93) = 0.83, p = .44, η2  = 0.02, which—of most relevance for our hypotheses—was qualified by a significant interaction between time and scent exposure, F(2.83, 131.76) = 3.05, p = .03, η2  = 0.06.

Evaluation: This does not look realistic. This pattern of p-values suggest massive selective reporting, and flexibility in the data analysis to yield p < .05.  

Vol 113(4)

Cortland, C. I., Craig, M. A., Shapiro, J. R., Richeson, J. A., Neel, R., & Goldstein, N. J. (2017). Solidarity through shared disadvantage: Highlighting shared experiences of discrimination improves relations between stigmatized groups. Journal of Personality and Social Psychology, 113(4), 547-567.

Study 1: 47 participants, in 2 between subject groups (party like it’s1999). Main result: Black participants’ support for same-sex marriage was somewhat higher when it was framed as a civil rights issue and similar to the experiences of Black Americans (M = 5.74, SD = 1.06) compared with when it was framed as a gay rights issue (M = 4.82, SD = 2.09), Brown-Forsythe t(28.22) = 1.83, p = .078, d = 0.57.

Study 2: 35 participants (15 vs 20 in two between subject conditions). Main results: As predicted, and replicating results from Experiment 1, Black participants in the shared experience with discrimination condition (framing gay marriage as a “civil rights issue”) expressed more support for same-sex marriage (M = 6.01, SD = 0.66) compared with participants in the control condition (framing gay marriage as a “gay rights issue”; M = 4.13, SD = 2.14), Brown-Forsythe t(23.65) = 3.72, p = .001, d = 1.12. Consistent with predictions, Black participants in the shared experience with discrimination condition reported greater empathy for same-sex couples (M = 5.70, SD = 1.33) than did participants in the control condition (M = 4.03, SD = 2.28), Brown-Forsythe t(31.42) = 2.72, p = .010, d = 0.86.

Study 3: 63 participants across 3 (yes, three) conditions. An effect of experimental condition emerged for attitudes toward lesbians, Brown-Forsythe F(2, 46.63) = 3.76, p = .031, and gay men, Brown-Forsythe F(2, 50.20) = 4.29, p = .019. Consistent with predictions, Games-Howell post hoc analyses revealed that compared with participants in the control condition (M = 5.71, SD = 1.14), participants in the blatant shared experience condition expressed somewhat more positive attitudes toward lesbians (M = 6.34, SD = 0.53, p = .070, d = 0.69).  [  5  ]  Similarly, participants in the blatant shared experience condition expressed more positive attitudes toward gay men (M = 5.97, SD = 0.71) than participants in the control condition (M = 5.40, SD = 1.13), although this effect was unreliable (p = .140, d = 0.59). Further, compared with participants in the control condition, participants in the subtle shared experience condition expressed more positive attitudes toward gay men (M = 6.14, SD = 0.69, p = .036, d = 0.78) and more positive attitudes toward lesbians (M = 6.30, SD = 0.75), although this effect was unreliable (p = .120, d = 0.61).

Study 4: Power analysis (1) expecting a d = 0.76 (!). Completely unreasonable, but ok. 102 participants. The results are really lovely: As shown in Table 1 and consistent with predictions, Asian American participants in the shared experience with discrimination condition expressed more perceived similarity with gay/lesbian people compared with those in the control condition, t(100) = 2.20, p = .030, d = 0.43 (see Table 1). Furthermore, conceptually replicating Experiment 3, Asian American participants in the shared experience with discrimination condition expressed more positive attitudes toward lesbians compared with those in the control condition, Brown-Forsythe t(90.57) = 2.44, p = .017, d = 0.48. In addition, Asian American participants in the shared experience with discrimination condition expressed more positive attitudes toward gay men compared to those in the control condition, Brown-Forsythe t(92.53) = 2.52, p = .014, d = 0.50. Finally, Asian American participants in the shared experience with discrimination condition expressed more support for gay and lesbian civil rights compared to those in the control condition, Brown-Forsythe t(90.84) = 2.09, p = .040, d = 0.41.

Study 5: 201 participants. Results: We conducted a 2 (mindset: similarity-seeking, neutral) × 2 (pervasive sexism: sexism salient, control) between-subjects ANOVA on participants’ anti-Black bias scores, revealing the predicted Pervasive Sexism × Mindset interaction, F(1, 184) = 5.55, p = .020, ηp 2  = .03. No main effects emerged (mindset: F(1, 184) < 1, p = .365, ηp 2  = .00; pervasive sexism: F(1, 184) < 1, p = .751, ηp 2  = .00). As seen in Figure 1 and consistent with predictions and prior research (Craig et al., 2012), among participants who described the series of landscapes in the neutral mindset condition, salient sexism led to greater anti-Black bias compared with the control condition (salient sexism article: M = 3.63, SD = 1.09; control article: M = 3.21, SD = 1.08), F(1, 184) = 4.06, p = .045, d = 0.39, 95% CI [0.01, 0.78]; see Figure 1). Furthermore, consistent with our prediction that manipulating a similarity-seeking mindset in the context of salient ingroup discrimination should reduce bias, among White women for whom sexism was made salient, inducing a similarity-seeking mindset (M = 3.12, SD = 1.07) led to less expressed anti-Black bias compared with inducing a neutral mindset, F(1, 184) = 5.91, p = .016, d = 0.48, 95% CI [0.09, 0.87].

Evaluation: This does not look realistic. This pattern of p-values suggest massive selective reporting, and flexibility in the data analysis to yield p < .05.  

Savani, K., & Job, V. (2017). Reverse ego-depletion: Acts of self-control can improve subsequent performance in indian cultural contexts. Journal of Personality and Social Psychology, 113(4), 589-607.

Study 1A: 77 ppn, result: As predicted, the Condition × Incongruence interaction was significant, B = −.055, SE = .023, z = 2.36, p = .018

Study 1B: 57 ppn, result: We found a significant effect of condition, B = 0.17, z = 1.97, p = .049,

Study 1c: 500 Mturkers. Main result: We found a significant effect of condition, B = 0.031, SE = .014, incidence rate ratio = 1.03, z = 2.15, p = .031

Note how the sample sizes change wildly in these studies, but the p-values stay just below .05? That’s a desk-reject if any of my bachelor students had been reviewers, but ok. Let’s read on.

Study 2: 180 Indians and 193 Americans on MTurk. Results: For Indians, we again found a main effect of incongruent trials, B = .12, SE = .009, z = 13.58, p < .001, and a Condition × Incongruence interaction, B = −.027, SE = .014, z = 1.99, p = .047. For Americans, we found a main effect of trial incongruence, B = .17, SE = .008, z = 21.27, p < .001, and a Condition × incongruence interaction, B = .022, SE = .011, z = 1.95, p = .051.

Study 3: 143 students in the lab. Results: As predicted, the Condition × Incongruence interaction was significant, B = −.046, SE = .015, z = 3.04, p = .002. The Condition × Incongruence interaction was significant, B = .034, SE = .012, z = 2.77, p = .006.

Hey, this looks good! So they do a follow-up analysis: Among Indian participants, however, we found a significant three-way interaction, B = −.0088, SE = .0044, z = 2.00, p = .045.

Study 4: 400 Mturkers from Inda, 400 from US. Results: We also found three two-way interactions: Culture × Strenuous versus nonstrenuous task condition, B = .048, SE = .021, z = 2.27, p = .023; Culture × Belief condition, B = −.051, SE = .021, z = 2.37, p = .018; and strenuous versus nonstrenuous task Condition × Belief condition, B = .062, SE = .021, z = 2.93, p = .003. The three-way Culture × Task Condition × Belief Condition interaction was nonsignificant, B = .038, SE = .043, z = .89, p = .38.

Evaluation: This does not look realistic. This pattern of p-values suggest massive selective reporting, and flexibility in the data analysis to yield p < .05.  

Vol 113(3)

Chou, E. Y., Halevy, N., Galinsky, A. D., & Murnighan, J. K. (2017). The goldilocks contract: The synergistic benefits of combining structure and autonomy for persistence, creativity, and cooperation. Journal of Personality and Social Psychology, 113(3), 393-412.

Study 1: 124 Mturkers. Results: An analysis of variance (ANOVA) revealed a significant effect of contract type on task persistence, F(2, 118) = 4.25, p = .01, partial η2  = .06. As predicted, the general-contract workers (M = 554.30 s, SD = 225.65) worked significantly longer than both the no-contract (M = 417.91 s, SD = 205.92), t(82) = 2.77, p = .007, Cohen’s d = .63, and the specific-contract workers (M = 455.66 s, SD = 177.15), t(63) = 1.97, p = .05, Cohen’s d = .49; the specific and no-contract groups did not differ, t(91) = .91, p = .36

Study 2: 188 MTurkers. Manipulation check:The contract manipulation was effective: Workers rated the general contract as less specific (M = 4.14, SD = .88) than the specific contract (M = 4.50, SD = 1.18), t(121.04) = −1.95, p = .05. (Phew! It worked). As predicted, workers’ contracts influenced their feelings of autonomy, F(2, 185) = 4.06, p = .01, partial η2  = .04: Workers who received the general contract (M = 4.92, SD = 1.01) or no contract at all (M = 4.98, SD = 1.07) felt more autonomy than workers who received the specific contract (M = 4.50, SD = 1.06), t(124) = 2.24, p = .02; Cohen’s d = .41; and, t(127) = 2.58, p = .01; Cohen’s d = .45, respectively. The general and no-contract groups did not significantly differ, t(119) = −.36, p = .23, suggesting that specific contracts reduced people’s feelings of autonomy. Ok, the next measures are not significant, let’s report them and call it ‘discriminant validity’(!). Contract type had no effect on feelings of competence, F(2, 185) = .67, p = .51, or belongingness, F(2, 185) = 1.53, p = .21. These results provide discriminant validity and support the importance of autonomy needs in driving the effects of contract specificity. And then: Time 1’s contracts influenced Time 2’s task persistence. Workers with a general contract at Time 1 worked almost twice as long at Time 2 (M = 914.06 s, SD = 1365.61) as workers who had received either the specific (M = 519.17 s, SD = 220.69), t(40.41) = 1.78, p = .08; Cohen’s d = .40, or no contract (M = 496.08, SD = 205.96), t(40.66) = 1.88, p = .06; Cohen’s d = .43. A planned contrast showed that workers who received the general contract persisted longer than workers in the other two conditions combined, t(93) = −2.20, p = .03.

Study 3a: 175 MTurk workers. Manipulation check. The contract manipulation was effective: Workers rated the general contract as less specific (M = 3.08, SD = 1.03) than the specific contract (M = 3.45, SD = .78), t(114) = −2.14, p = .03, Cohen’s d = .40. Phew! The manipulation check worked again! Lucky us! Results: Replicating our findings from Experiment 2, workers’ contracts influenced their feelings of autonomy, F(2, 172) = 2.94, p = .05, partial η2  = .03: Workers who received the general contract (M = 3.20, SD = .96) felt greater autonomy than workers who received the specific contract (M = 2.80, SD = .90; t(114) = 2.29, p = .02, Cohen’s d = .42). Those who did not receive any contract (M = 3.12, SD = .97) felt marginally more autonomy than those who received the specific contract t(118) = 1.89, p = .06, Cohen’s d = .34.

Study 3b: 82 students. Results:  Those who thought that the lab’s code of conduct was more general felt more autonomy (M = 3.68, SD = .73) than those who thought the lab code of conduct was more specific (M = 3.35, SD = .73), t(80) = 2.01, p = .04, Cohen’s d = .45. As predicted, we found a significant interaction between contract condition and perceived structure on autonomy (B = −.37, SE = .16, t = −2.32, p = .02). Bootstrapping analysis verified that the effect of general contract on autonomy is significant only when people perceive a sense of structure (95% bias-corrected bootstrapped CI [−1.21, −.07]). Likewise, we found a significant interaction between contract condition and perceived structure on intrinsic motivation (B = −.42, SE = .18, t = −2.36, p = .02).

Study 3C: Single-indicator path modeling using nonparametric bootstrapping indicates that the proposed model fit the data well (comparative fit index [CFI] = 0.98, root-mean-square error of approximation [RMSEA] = 0.05), χ2 (3) = 6.67, p = .08,

Study 4: 149 undergraduates. Results: Participants who received the general legal clauses worked significantly longer (M = 590.08 s, SD = 332.44) than those who received the specific legal clauses (M = 415.12 s, SD = 217.01), F(1, 145) = 14.66, p < .001, Cohen’s d = .62. The opposite pattern emerged for the technical clause manipulation: Participants who received the general technical clause spent less time on the task (M = 443.29 s, SD = 184.38) as compared with those who received the specific technical clauses (M = 552.37 s, SD = 357.41), F(1, 145) = 6.27, p = .01, Cohen’s d = .38. [These results on their own would be ok, if the first test did not yield a slightly too large effect size].

Study 5A: 91 MTurkers. Results: As predicted, the general contract led workers to produce more original ideas (M = 4.02, SD = .89) than the specific contract did (M = 3.57, SD = 1.11), t(89) = 2.14, p = .03, Cohen’s d = .45. General contracts also led workers to produce more unique ideas (M = 8.29, SD = 3.71 vs. M = 6.55, SD = 3.85), t(89) = 2.18, p = .03, Cohen’s d = .46. We replicated the main effect of general contracts on idea generation with a separate sample (80 MTurk workers; mean age = 37.95, SD = 12.34; 67% female), using slightly different contracts. Workers who received the general contract generated more unique uses than those who received the specific contract did (M = 8.02, SD = 3.8 vs. M = 6.43, SD = 2.86), t(78) = 2.15, p = .03, d = .47.

Study 5B: 143 MTurkers. Results: As predicted, workers in the general contract condition solved significantly more problems correctly (M = 1.38, SD = .70) than workers in the specific contract condition (M = 1.07, SD = .73), t(141) = 2.61, p = .01, Cohen’s d = .43. The general contract (M = 4.51, SD = 1.09) also produced stronger intrinsic motivation than the specific contract (M = 4.15, SD = 1.04), t(141) = 1.95, p = .05, Cohen’s d = .34.

Experiment 6. As predicted, participants who received the general contract cooperated at a significantly higher rate (M = 84%, SD = 36%) than those who received the specific legal clauses (M = 70%, SD = 46%), χ2 (1) = 4.60, p = .03.

Evaluation: This does not look realistic. This pattern of p-values suggest massive selective reporting, and flexibility in the data analysis to yield p < .05.  

Prediction and Validity of Theories

What is the goal of data collection? This is a simple question, and as researchers we collect data all the time. But the answer to this question is not straightforward. It depends on the question that you are asking of your data. There are different questions you can ask from your data, and therefore, you can have different goals when collecting data. Here, I want to focus on collecting data to test scientific theories. I will be quoting a lot from De Groot’s book Methodology (1969), especially Chapter 3. If you haven’t read it, you should – I think it is the best book about doing good science that has ever been written.

When you want to test theories, the theory needs to make a prediction, and you need to have a procedure that can evaluate verification criteria. As De Groot writes: “A theory must afford at least a number of opportunities for testing. That is to say, the relations stated in the model must permit the deduction of hypotheses which can be empirically tested. This means that these hypotheses must in turn allow the deduction of verifiable predictions, the fulfillment or non-fulfillment of which will provide relevant information for judging the validity or acceptability of the hypotheses” (§ 3.1.4).

This last sentence is interesting – we collect data, to test the ‘validity’ of a theory. We are trying to see how well our theory works when we want to predict what unobserved data looks like (whether these are collected in the future, or in the past, as De Groot remarks). As De Groot writes: “Stated otherwise, the function of the prediction in the scientific enterprise is to provide relevant information with respect to the validity of the hypothesis from which it has been derived.” (§ 3.4.1).

To make a prediction that can be true or false, we need to forbid certain states of the world and allow others. As De Groot writes: “Thus, in the case of statistical predictions, where it is sought to prove the existence of a causal factor from its effect, the interval of positive outcomes is defined by the limits outside which the null hypothesis is to be rejected. It is common practice that such limits are fixed by selecting in advance a conventional level of significance: e.g., 5 %, 1 %, or .1 % risk of error in rejecting the assumption that the null hypothesis holds in the universe under consideration. Though naturally a judicious choice will be made, it remains nonetheless arbitrary. At all events, once it has been made, there has been created an interval of positive outcome, and thus a verification criterion. Any outcome falling within it stamps the prediction as 'proven true.” (§ 3.4.2). Note that if you prefer, you can predict an effect size with some accuracy, calculate a Bayesian highest density interval that excludes some value, or a Bayes factor that is larger than some cut-off – as long as your prediction can be either confirmed or not confirmed.

Note that the prediction gets a ‘proven true’ stamp – the theory does not. In this testing procedure, there is no direct approach from the ‘proven true’ stamp to a ‘true theory’ conclusion. Indeed, the latter conclusion is not possible in science. We are mainly indexing the ‘track record’ of a theory, as Meehl (1990) argues: “The main way a theory gets money in the bank is by predicting facts that, absent the theory, would be antecedently improbable.” Often (e.g., in non-experimental settings) rejecting a null hypothesis with large sample sizes is not considered a very improbable event, but that is another issue (see also the definition of a severe test by Mayo (1996, 178): a passing result is a severe test of hypothesis H just to the extent that it is very improbable for such a passing result to occur, were H false).

Regardless of how risky the prediction we made was, when we then collect data, and test the hypothesis, we either confirm our prediction, or we do not confirm our prediction. In frequentist statistics, we add the outcome of this prediction to the ‘track record’ of our theory, but we can not draw conclusions based on any single study. As Fisher (1926, 504) writes: “if one in twenty does not seem high enough odds, we may, if we prefer it, draw the line at one in fifty (the 2 per cent point), or one in a hundred (the 1 per cent point). Personally, the writer prefers to set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance” (italics added).

The study needs to be ‘properly designed’ to ‘rarely' fail to give a level of evidence – which despite Fisher’s dislike for Neyman-Pearson statistics, I can read in no other way than to make sure you run well-powered studies for whatever happens to be your smallest effect size of interest. In other words: When testing the validity of theories through predictions, where you keep track of a ‘track record’ of predictions, you need to control your error rates to efficiently distinguish hits from misses. Design well-powered studies, and do not fool yourself by inflating the probability of observed in false positive.

I think that when it comes to testing theories, assessing the validity through prediction is extremely (and for me, perhaps the most) important. We don’t want to fool ourselves when we test the validity of our theories. An example of ‘fooling yourself’ are the studies on pre-cognition by Daryl Bem (2011). An example of a result I like to use in workshops is the following result of Study 1 where people pressed a left or right button to predict whether a picture was hidden behind a left or right curtain.

If we take this study as it is (without pre-registration) it is clear there are 5 tests (for erotic, neutral, negative, positive, and ‘romantic but non-erotic’ pictures). A Bonferroni correction would lead us to use an alpha level of 0.01 (an alpha of 0.05/5 tests) and the result (0.01, but more precisely 0.013) would not be enough to support our prediction, given the pre-specified alpha level. Note that Bem (Bem, Utts, and Johnson, 2011) explicitly says this test was predicted. However, I see absolutely no reason to believe Bem without a pre-registration document for the study.

Bayesian statistics do not provide a solution when analyzing this pre-cognition experiment. As Gelman and Loken (2013) write about this study (I just realized this ‘Garden of Forking paths’ paper is unpublished, but has 150 citations!): “we can still take this as an observation that 53.1% of these guesses were correct, and if we combine this with a flat prior distribution (that is, the assumption that the true average probability of a correct guess under these conditions is equally likely to be anywhere between 0 and 1) or, more generally, a locally-flat prior distribution, we get a posterior probability of over 99% that the true probability is higher than 0.5; this is one interpretation of the one-sided p-value of 0.01.” The use of Bayes factors that quantify model evidence provides no solution. Where Wagenmakers and colleagues argue based on ‘default’ Bayesian t-tests that the null-hypothesis is supported, Bem, Utts, and Johnson (2011) correctly point out this criticism is flawed, because the default Bayesian t-tests use completely unrealistic priors for pre-cognition research (and most other studies published in psychology, for that matter).

It is interesting that the best solution Gelman and Loken come up with is that “perhaps researchers can perform half as many original experiments in each paper and just pair each new experiment with a preregistered replication”. What matters is not just the data, but the procedure used to collect the data. The procedure needs to be able to demonstrate a strong predictive validity, which is why pre-registration is such a great solution to many problems science faces. Pre-registered studies are the best way we have to show you can actually predict something – which gets your theory money in the bank.

If people ask me if I care about evidence, I typically say: ‘mwah’. For me, evidence is not a primary goal of doing research. Evidence is a consequence of demonstrating that my theories have high validity as I test predictions. It is important to end up with, and it can be useful to try to quantify model evidence through likelihoods or Bayes factors, if you have good models. But if I am able to show that I can confirm predictions in a line of pre-registered studies, either by showing my p-value is smaller than an alpha level, a Bayesian highest density interval excludes some value, a Bayes factor is larger than some cut-off, or by showing the effect size is close enough to some predicted value, I will always end up with strong evidence for the presence of some effect. As De Groot (1969) writes: “If one knows something to be true, one is in a position to predict; where prediction is impossible, there is no knowledge.”

References

Bem, D. J. (2011). Feeling the future: experimental evidence for anomalous retroactive influences on cognition and affect. Journal of Personality and Social Psychology, 100(3), 407–425. https://doi.org/10.1037/a0021524

Bem, D. J., Utts, J., & Johnson, W. O. (2011). Must psychologists change the way they analyze their data? Journal of Personality and Social Psychology, 101(4), 716–719. https://doi.org/10.1037/a0024777

Gelman, A., & Loken, E. (2013). The garden of forking paths: Why multiple comparisons can be a problem, even when there is no “fishing expedition” or “p-hacking” and the research hypothesis was posited ahead of time. Department of Statistics, Columbia University.

De Groot, A. D. (1969). Methodology. The Hague: Mouton & Co.

Mayo, D. G. (1996). Error and the growth of experimental knowledge. University of Chicago Press.

Wagenmakers, E.-J., Wetzels, R., Borsboom, D., & van der Maas, H. L. J. (2011). Why psychologists must change the way they analyze their data: the case of psi: comment on Bem (2011). Journal of Personality and Social Psychology, 100(3), 426–432. https://doi.org/10.1037/a0022790

The Costs and Benefits of Replications

This blog post is based on a pre-print by Coles, Tiokhin, Scheel, Isager, and Lakens “The Costs and Benefits of Replications”, submitted to Behavioral Brain Sciences as a commentary on “Making Replication Mainstream”.

In a summary of recent discussions about the role of direct replications in psychological science, Zwaan, Etz, Lucas, and Donnellan (2017) argue that replications should be more mainstream. The debate about the importance of replication research is essentially driven by disagreements about the value of replication studies, in a world where we need to carefully think about the best way to allocate limited resources when pursuing scientific knowledge. The real question, we believe, is when replication studies are worthwhile to perform.

Goldin-Meadow stated that "it’s just too costly or unwieldy to generate hypotheses on one sample and test them on another when, for example, we’re conducting a large field study or testing hard-to-find participants" (2016). A similar comment is made by Tackett and McShane (2018) in their comment on ZELD: “Specifically, large-scale replications are typically only possible when data collection is fast and not particularly costly, and thus they are, practically speaking, constrained to certain domains of psychology (e.g., cognitive and social).”

Such statements imply a cost-benefit analysis. But these scholars do not quantify their costs and benefits. They hide their subjective expected utility (what is a large-scale replication study worth to me) behind absolute statements, as they write “is” and “are” but really mean “it is my subjective belief that”. Their statements are empty, scientifically speaking, because they are not quantifiable. What is “costly”? We can not have a discussion about such an important topic if researchers do not specify their assumptions in quantifiable terms.

Some studies may be deemed valuable enough to justify even quite substantial investments to guarantee that a replication study is performed. For instance, because it is unlikely that anyone will build a Large Hadron Collider to replicate the studies at CERN, there are two detectors (ATLAS and CMS) so that independent teams can replicate each other’s work. That is, not only do these researchers consider it important to have a very low (5 sigma) alpha level when they analyze data, they also believe it is worthwhile to let two team independently do the same thing. As a physicist remarks: “Replication is, in the end, the most important part of error control. Scientists are human, they make mistakes, they are deluded, and they cheat. It is only through attempted replication that errors, delusions, and outright fraud can be caught.” Thus, high cost is not by itself a conclusive argument against replication. Instead, one must make the case that the benefits do not justify the costs. Again, I ask: what is “costly”?

Decision theory is a formal framework that allows researchers to decide when replication studies are worthwhile. It requires researchers to specify their assumptions in quantifiable terms. For example, the expected utility of a direct replication (compared to a conceptual replication) depends on the probability that a specific theory or effect is true. If you believe that many published findings are false, then directly replicating prior work may be a cost-efficient way to prevent researchers from building on unreliable findings. If you believe that psychological theories usually make accurate predictions, then conceptual extensions may lead to more efficient knowledge gains than direct replications. Instead of wasting time arguing about whether direct replications are important or whether conceptual replications are important, do the freaking math. Tell us at which probability that H0 is true you think it is efficient enough to weed out false positives from the literature through direct replications. Show us, by pre-registering all your main analyses, that you are building on strong theories that allow you to make correct predictions with a 92% success rate, and that you therefore do not feel direct replications are the more efficient way to gain knowledge in your area.

I am happy to see our ideas about the importance of using decision theory to determine when replications are important enough to perform were independently replicated in this commentary on ZELD by Hardwicke, Tessler, Peloquin, and Frank. We have collaboratively been working on a manuscript to specify the Replication Value of replication studies for several years, and with the recent funding I received, I’m happy that we can finally dedicate the time to complete this work. I look forward to scientists explicitly thinking about the utility of the research they perform. This is an important question, and I can’t wait for our field to start discussing ways to answer how we can quantify the utility of the research we perform. This will not be easy. But unless you never think about how to spend your resources, you are making these choices implicitly all the time, and this question is too important to give up without even trying. In our pre-print, we illustrate how all concerns raised against replication studies basically boil down to a discussion about their costs and benefits, and how formalizing these costs and benefits would improve the way researchers discuss this topic.

Understanding common misconceptions about p-values

A p-value is the probability of the observed, or more extreme, data, under the assumption that the null-hypothesis is true. The goal of this blog post is to understand what this means, and perhaps more importantly, what this doesn’t mean. People often misunderstand p-values, but with a little help and some dedicated effort, we should be able explain these misconceptions. Below is my attempt, but if you prefer a more verbal explanation, I can recommend Greenland et al. (2016).

First, we need to know what ‘the assumption that the null-hypothesis is true’ looks like. Although the null-hypothesis can be any value, here we will assume the null-hypothesis is specified as a difference of 0. When this model is visualized in text-books, or in power-analysis software such as g*power, you often see a graph like the one below, with t-values on the horizontal axis, and a critical t-value somewhere around 1.96. For a mean difference, the p-value is calculated based on the t-distribution (which is like a normal distribution, and the larger the sample size, the more similar the two become). I will distinguish the null hypothesis (the mean difference in the population is exactly 0) from the null-model (a model of the data we should expect when we draw a sample when the null-hypothesis is true) in this post. 

I’ve recently realized that things become a lot clearer if you just plot these distributions as mean differences, because you will more often think about means, than about t-values. So below, you can see a null-model, assuming a standard deviation of 1, for a t-test comparing mean differences (because the SD = 1, you can also interpret the mean differences as a Cohen’s d effect size). 

The first thing to notice is that we expect that the mean of the null-model is 0: The distribution is centered on 0. But even if the mean in the population is 0, that does not imply every sample will give a mean of exactly zero. There is variation around the mean, as a function of the true standard deviation, and the sample size. One reason why I prefer to plot the null-model in raw scores instead of t-values is that you can see how the null-model changes, when the sample size increases.

When we collect 5000 instead of 50 observations, we see the null-model is still centered on 0 – but in our null-model we now expect most values will fall very close around 0. Due to the larger sample size, we should expect to observe mean differences in our sample closer to 0 compared to our null-model when we had only 50 observations.

Both graphs have areas that are colored red. These areas represent 2.5% of the values in the left tail of the distribution, and 2.5% of the values in the right tail of the distribution. Together, they make up 5% of the most extreme mean differences we would expect to observe, given our number of observations, when the true mean difference is exactly 0 – representing the use of an alpha level of 5%. The vertical axis shows the density of the curves.

Let’s assume that in the figure visualizing the null model for N = 50 (two figures up) we observe a mean difference of 0.5 in our data. This observation falls in the red area in the right tail of the distribution. This means that the observed mean difference is surprising, if we assume that the true mean difference is 0. If the true mean difference is 0, we should not expect such a extreme mean difference very often. If we calculate a p-value for this observation, we get the probability of observing a value more extreme (in either tail, when we do a two-tailed test) than 0.5.

Take a look at the figure that shows the null-model when we have collected 5000 observations (one figure up), and imagine we would again observe a mean difference of 0.5. It should be clear that this same difference is even more surprising than it was when we collected 50 observations.

We are now almost ready to address common misconceptions about p-values, but before we can do this, we need to introduce a model of the data when the null is not true. When the mean difference is not exactly 0, the alternative hypothesis is true – but what does an alternative model look like?

When we do a study, we rarely already know what the true mean difference is (if we already knew, why would we do the study?). But let’s assume there is an all-knowing entity. Following Paul Meehl, we will call this all-knowing entity Omniscient Jones. Before we collect our sample of 50 observations, Omniscient Jones already knows that the true mean difference in the population is 0.5. Again, we should expect some variation around this true mean difference in our small sample. The figure below again shows the expected data pattern when the null-hypothesis is true (now indicated by a grey line) and it shows an alternative model, assuming a true mean difference of 0.5 exists in the population (indicated by a black line).

But Omniscient Jones could have said the true difference was much larger. Let’s assume we do another study, but now before we collect our 50 observations, Omniscient Jones tells us that the true mean difference is 1.5. The null model does not change, but the alternative model now moves over to the right. 

 

Now, we are finally ready to address some common misconceptions about p-values. Before we look at misconceptions in some detail, I want to remind you of one fact that is easy to remember, and will enable you to recognize many misconceptions about p-values: p-values are a statement about the probability of data, not a statement about the probability of a theory. Whenever you see p-values interpreted as a probability of a theory or a hypothesis, you know something is not right. Now let’s take a look at why this is not right.

1) Why a non-significant p-value does not mean that the null-hypothesis is true.

Let’s take a concrete example that will illustrate why a non-significant result does not mean that the null-hypothesis is true. In the figure below, Omniscient Jones tells us the true mean difference is again 0.5. We have observed a mean difference of 0.35. This value does not fall within the red area (and hence, the p-value is not smaller than our alpha level, or p > .05). Nevertheless, we see that observing a mean difference of 0.35 is much more likely under the alternative model, than under the null-model. 

All the p-value tells us is that this value is not extremely surprising, if we assume the null-hypothesis is true. A non-significant p-value does not mean the null-hypothesis true. It might be, but it is also possible that the data we have observed is more likely when the alternative hypothesis is true, than when the null-hypothesis is true (as in the figure above).

2) Why a significant p-value does not mean that the null-hypothesis is false.

Imagine we generate a series of numbers in R using the following command:

rnorm(n = 50, mean = 0, sd = 1)

This command generates 50 random observations from a distribution with a mean of 0 and a standard deviation of 1. We run this command once, and we observe a mean difference of 0.5. We can perform a one-sample t-test against 0, and this test tells us, with a p < .05, that the data we have observed is surprisingly extreme, assuming the random number generator in R functions as it should.

Should we decide to reject the null-hypothesis that the random number generator in R works? That would be a bold move indeed! We know that the probability of observing surprising data, assuming the null hypothesis is true, has a maximum of 5% when our alpha is 0.05. What we can conclude, based on our data, is that we have observed an extreme outcome, that should be considered surprising. But such an outcome is not impossible when the null-hypothesis is true. And in this case, we really don’t even have an alternative hypothesis that can explain the data (beyond perhaps evil hackers taking over the website where you downloaded R).

This misconception can be expressed in many forms. For example, one version states that the p-value is the probability that the data were generated by chance. Note that this is just a sneaky way to say: The p-value is the probability that the null hypothesis is true, and we observed an extreme p-value just due to random variation. As we explained above, we can observe extreme data when we are basically 100% certain that the null-hypothesis is true (the random number generator in R works as it should), and seeing extreme data once should not make you think the probability that the random number generator in R is working is less than 5%, or in other words, that the probability that the random number generator in R is broken is now more than 95%.

Remember: P-values are a statement about the probability of data, not a statement about the probability of a theory or a hypothesis.

3) Why a significant p-value does not mean that a practically important effect has been discovered.

If we plot the null-model for a very large sample size (N = 100000) we see that even very small mean differences (here, a mean difference of 0.01) will be considered ‘surprising’. We have such a large sample size, that all means we observe should fall very close around 0, and even a difference of 0.01 is already considered surprising, due to our substantial level of accuracy because we collected so much data. 

Note that nothing about the definition of a p-value changes: It still correctly indicates that, if the null-hypothesis is true, we have observed data that should be considered surprising. However, just because data is surprising, does not mean we need to care about it. It is mainly the verbal label ‘significant’ that causes confusion here – it is perhaps less confusing to think of a ‘significant’ effect as a ‘surprising’ effect (as long as the null-model is realistic - which is not automatically true).

This example illustrates why you should always report and interpret effect sizes, with hypothesis tests. This is also why it is useful to complement a hypothesis test with an equivalence test, so that you can conclude the observed difference is surprisingly small if there is no difference, but the observed difference is also surprisingly closer to zero, assuming there exists any effect we consider meaningful (and thus, we can conclude the effect is equivalence to zero).

4) If you have observed a significant finding, the probability that you have made a Type 1 error (a false positive) is not 5%.

Assume we collect 20 observations, and Omniscient Jones tells us the null-hypothesis is true. This means we are sampling from the following distribution:

If this is our reality, it means that 100% of the time that we observe a significant result, it is a false positive. Thus, 100% of our significant results are Type 1 errors. What the Type 1 error rate controls, is that from all studies we perform when the null is true, not more than 5% of our observed mean differences will fall in the red tail areas. But when they have fallen in the tail areas, they are always a Type 1 error. After observing a significant result, you can not say it has a 5% probability of being a false positive. But before you collect data, you can say you will not conclude there is an effect, when there is no effect, more than 5% of the time, in the long run.

5) One minus the p-value is not the probability of observing another significant result when the experiment is replicated.

It is impossible to calculate the probability that an effect will replicate, based on the p-value, and as a consequence, the p-value can not inform us about the p-value we will observe in future studies. When we have observed a p-value of 0.05, it is not 95% certain the finding will replicate. Only when we make additional assumptions (e.g., the assumption that the alternative effect is true, and the effect size that was observed in the original study is exactly correct) can we model the p-value distribution for future studies.

It might be useful to visualize the one very specific situation when the p-value does provide the probability that future studies will provide a significant p-value (even though in practice, we will never know if we are in this very specific situation). In the figure below we have a null-model and alternative model for 150 observations. The observed mean difference falls exactly on the threshold for the significance level. This means the p-value is 0.05. In this specific situation, it is also 95 probable that we will observe a significant result in a replication study, assuming there is a true effect as specified by the alternative model. If this alternative model is true, 95% (1-p) of the observed means will fall on the right side of the observed mean in the original study (we have a statistical power of 95%), and only 5% of the observed means will fall in the blue area (which contains the Type 2 errors). 

This very specific situation is almost always not your reality. It is not true when any other alternative hypothesis is correct. And it is not true when the the null-hypothesis is true. In short, the p-value basically never, except for one very specific situation when the alternative hypothesis is true and of a very specific size you will never know you are in, gives the probability that a future study will once again yield a significant result.

Conclusion

Probabilities are confusing, and the interpretation of a p-value is not intuitive. Grammar is also confusing, and not intuitive. But where we practice grammar in our education again and again and again until you get it, we don’t practice the interpretation of p-values again and again and again until you get it. Some repetition is probably needed. Explanations of what p-values mean are often verbal, and if there are figures, they use t-value distributions we are unfamiliar with. Instead of complaining that researchers don’t understand what p-values mean, I think we should try to explain common misconceptions multiple times, in multiple ways.

 R code for the figures

Daniel Lakens, 2017

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.